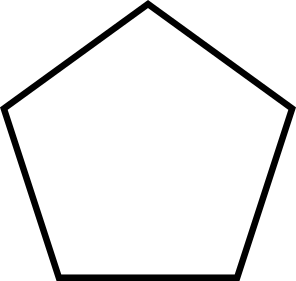
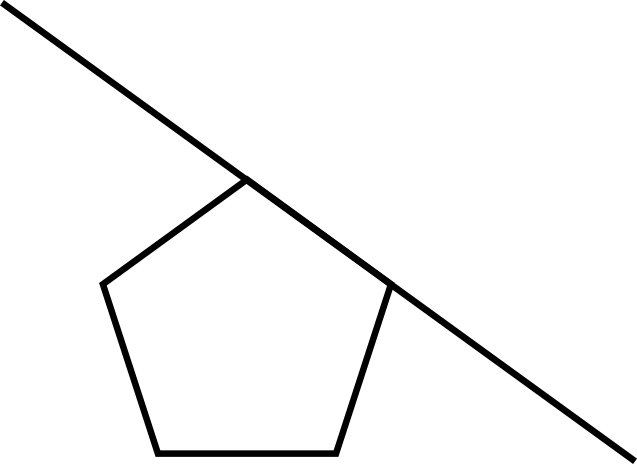
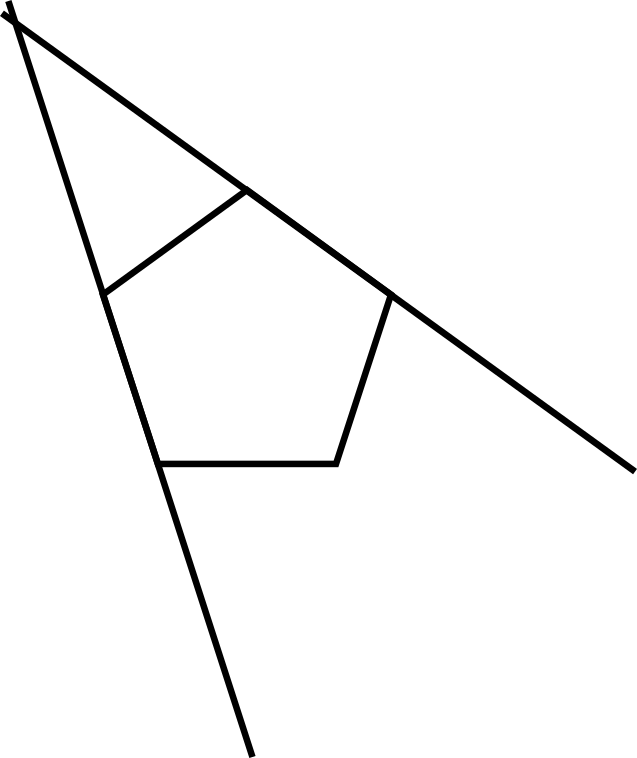
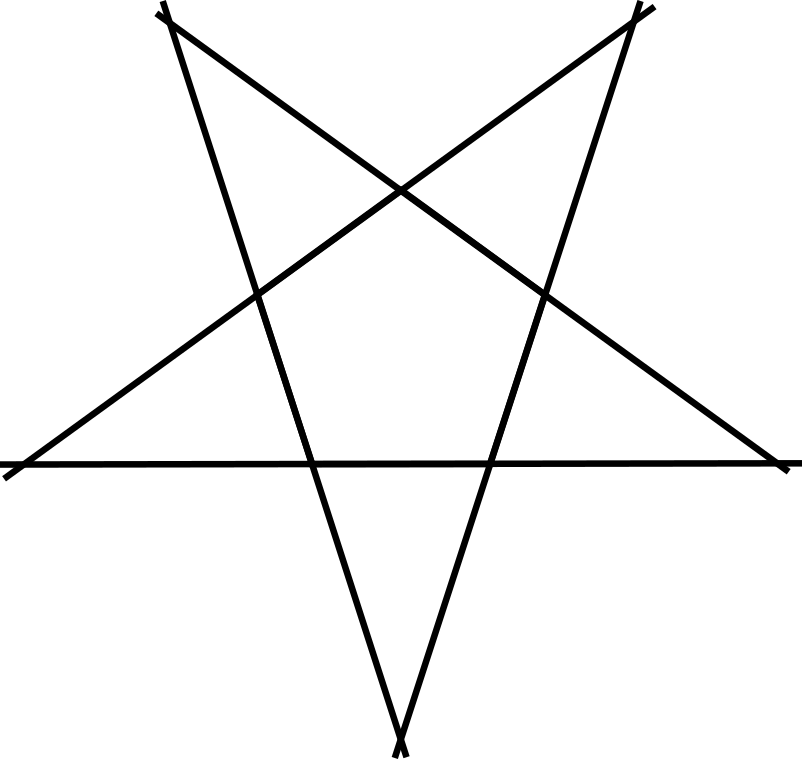
Technically all that stellation is, is the new polyhedron formed by the intersection of it's faces after you expand them. Maybe that still sounds intimidating or unintuitive, it might be easier to visualize in two dimensions; if you look at a pentagon and extend it's edges(instead of it's faces) you see that they will eventually cross, all these crossings form a pentagram(shown below). You can keep extending the edges but they will never intersect again(when you move to 3d polyhedra or even just polygons with more sides there will be multiple crossings and thus multiple possible stellations).

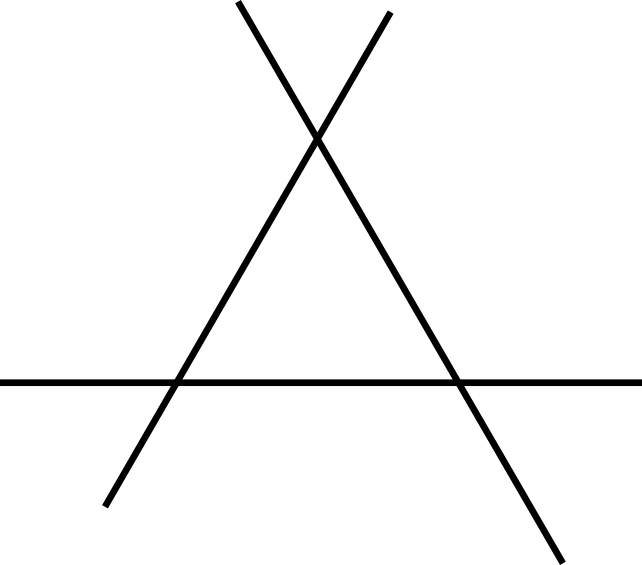This doesn't work for all polytopes as you can see if you look at things like a triangle, square, tetrahedron, or cube as the lines never cross.

Now for an example in three dimensions it's easiest to look at the octahedron(left). So first things first by our definition before we expand the faces. Small note but just like in 2d you don't deform the rest of the polyhedron(like the image on the left bellow). For these visual demonstrations I initially don't expand the faces the amount they need to fully meet as it makes it far to difficult to see things but in reality you can extend the face into an infinite plane. As a result you don't need to worry about the shape of the initial face, just the plane that it's in.

Now remember we're looking for intersections between faces so let's look at the different kinds of faces and how they interact roughly one by one. Different kinds of faces not meaning different polygons as the faces are the same(the octahedron is a platonic solid after all) so let's expand the top face and look at the other faces in regard to that and then we can apply what we learn from there to all of the other faces. First things first there's a face directly opposite to the top face that is parallel so we know that one will never intersect with our face. That leaves two categories of faces here, the 3 faces connected to the edges(left bellow)and the ones that share vertices(right bellow).

What we're gonna do here is track where these faces intersect with the top plane by looking at the top plane in 2d and showing the intersections as lines. Because the faces can expand infinitely so can the lines that represent the intersections. So first you can see that an anjacent face(ones connected along edges with the top) when extended just extends along the line of the original top faces triangle(you can't see it on the right and the lines of it on the right are not intersections and thus are slightly greyer).

If you extend the other kind of face, the ones that only share a vertice with the top, then the intersection is essentially tangent to the vertice that the face shared with the top face(not sure if that terminology holds here but you can see what it looks like) it's also parallel to the other face we extended.

So if we extend all of the edge adjacent faces the intersections with the top face just form the initial triangle of the top face in our 2d diagram. However in a sort of preview of what is to come if you look in 3d they intersect above the top face too. If we extend them the rest of the way to where they all meet at a new point and take only the parts of the extended face that properly intersect then we get this little tetrahedron/pyramid added on top of the octahedron. Now I could skip forward here and say just do that for all the faces and it would get us the final stellation but you can't easily do that with other polyhedra so instead I'm showing a more generalizable way of understanding stellation using that 2d diagram of the intersections with a single face(which is called a stellation diagram btw).

So instead let's look at when you extend all 3 faces that only share a corner with the top face. You can see on the stellation diagram that this makes a larger triangle around the base triangle. Also looking ahead a bit you can notice that again when you only expand these specific faces they again meet at a point but this time they do so at 4 different points and create a large tetrahedron that encompases the entire octahedron. The same happens if you choose the opposite four faces(look back at the picture highlighting the 4 corner adjacent faces and you may notice that choosing the other 4 gets you a selection congruent to the other one(the same but in a different orientation)), for the sake of preserving a consistent view angle you only see the one face facing us but it's the same tetrahedron as before, just in a different orientation.

So the whole stellation diagram is all of the 2d sections together. The whole thing with a stellation diagram is that you know that every face has these intersections so you can choose parts of the diagram to be part of a certain stellation and replace each face with your selection, that is if your selection results in a fully closed polyhedron that is. In this case you only have the coice of the original triangle or the three external triangles but for more larger polyhedra there are many more options.

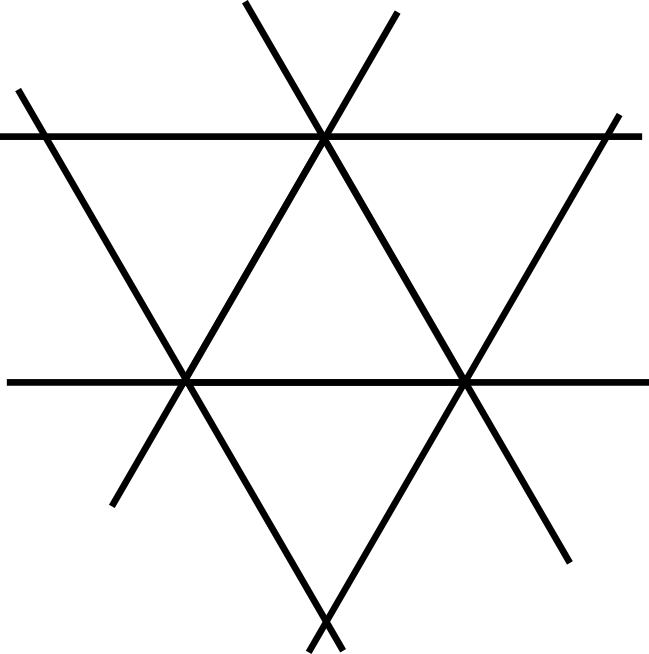
So there we have it, the stellation of the octahedron, aka the stella octangula. You may be able to see that like I alluded to before you can think of this polyhedron as just sticking a pyramid on each face of the octahedron or alternatively and often more usefully you can see that there are larger triangles around each original face of the octahedron. The other cool thing about the stella octangula is that it can be seen as a compund of two tetrahedra, which earlier you saw can come from stellating a specific half of the octahedron(interestingly the tetrahedron's dual is itself but in a different orientation and the stella octangula is also what you get if you combine a tetrahedron with it's dual). There was a misconception online that I saw once where someone refered to the great stellated dodecahedron as a stellated icosahedron because it looks exactly like if you took an icosahedron and added pyramids to the faces(not constructed with equilateral triangles but nonetheless pyramids) but as the actual name suggests it's a stellation of the dodecahedron. That's part of why I tried to emphasize using the interpretation of a stellation diagram because though in this case and others you can just extend the edge adjacent faces and make pyramids around each face stellation is more than just that.